PyTorch Housing Price Prediction Demo (Multi-feature)
This tutorial demonstrates how to build a PyTorch housing price prediction model using multiple features such as area, number of bedrooms, and house type.
You will learn how to:
- Generate synthetic multi-feature housing data
- Train a linear regression model with PyTorch
- Standardize and de-standardize features and targets
- Compare learned weights with ground truth
- Predict the price of a new house sample
By the end, you’ll understand how PyTorch can be applied to structured data regression tasks beyond image classification.
Part 1: Import Dependencies and Set Random Seed
- Import PyTorch, NumPy and StandardScaler
- Set a random seed to ensure consistent results across runs
import torch
from torch import nn
import numpy as np
from sklearn.preprocessing import StandardScaler
torch.manual_seed(0) # Set random seed for reproducibility
Part 2: Generate Simulated Housing Feature Data
- Manually generate housing data: area, number of bedrooms, and house type
Xhas shape(500, 5), where each row is a 5-dimensional feature vector for a sample
# Simulate 500 housing samples
n = 500
# Area in square meters
area = torch.normal(150.0, 40.0, size=(n, 1))
# Number of bedrooms: integers from 1 to 4
bed = torch.randint(1, 5, (n, 1)).float()
# House type: 0 = detached, 1 = townhouse, 2 = condo
types = torch.randint(0, 3, (n, 1))
type_onehot = nn.functional.one_hot(types.squeeze(), num_classes=3).float()
# Combine all features: area, bedrooms, house type → X
# Final shape: (500, 5)
X_raw = torch.cat([area, bed, type_onehot], dim=1)
Part 3: Generate Target Variable y (Simulated House Prices)
We assume ground truth weights for different housing features (area, bedrooms, house type), then add Gaussian noise to simulate real-world uncertainty.
- Use preset weights and bias to generate the target price
- Add Gaussian noise (std = 50,000) to simulate real-world noise
# Assume ground truth weights
true_w = torch.tensor([2000.0, 15000.0, 200000.0, 0.0, -200000.0])
# Bias term (base price)
true_b = 100000.0
# Add Gaussian noise
y_raw = X_raw @ true_w + true_b + torch.normal(0, 50000, (n,))
Part 4: Standardize Features and Labels
Standardization ensures each feature contributes fairly during training and improves gradient descent stability.
scaler_X = StandardScaler()
X = torch.tensor(scaler_X.fit_transform(X_raw.numpy()), dtype=torch.float32)
scaler_y = StandardScaler()
y = torch.tensor(scaler_y.fit_transform(y_raw.view(-1, 1)).squeeze(), dtype=torch.float32)
Part 5: Define Linear Regression Model in PyTorch
- Define a linear model using PyTorch’s
nn.Linear - Use MSE as the loss function
# Linear regression model: input features = 5, output = 1 (price)
net = nn.Linear(X.shape[1], 1)
# Loss function: Mean Squared Error
loss_fn = nn.MSELoss()
# Optimizer: Stochastic Gradient Descent
optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
Part 6: Train the Model
We use Adam optimizer with Mean Squared Error (MSE) loss for training. Although this is a small dataset, the setup mimics real regression workflows.
- Run 3000 iterations (epochs) of training
- Full-batch training: using all samples in each iteration
for epoch in range(3000):
pred = net(X).squeeze() # Make predictions
loss = loss_fn(pred, y) # Compute loss
optimizer.zero_grad() # Clear previous gradients
loss.backward() # Backpropagation
optimizer.step() # Update model parameters
if epoch % 300 == 0: #print the loss every 300 epochs
print(f"Epoch {epoch}, Loss: {loss.item():.4f}")
Part 7: De-standardize Results and Compare with Ground Truth
After training, we rescale the learned weights and bias back to the original scale, and compare them with the assumed true parameters.
- After training, print the learned weights and bias
- Compare them with
true_wandtrue_bto check if the model learned correctly
w_learned = net.weight.data.squeeze().numpy()
b_learned = net.bias.data.item()
# Convert back to original scale
w_learned_rescaled = scaler_y.scale_[0] * w_learned / scaler_X.scale_
b_learned_rescaled = (
scaler_y.scale_[0] * b_learned
+ scaler_y.mean_[0]
- np.sum(w_learned_rescaled * scaler_X.mean_)
)
# Print and Compare
print("Learned weights:", w_learned_rescaled)
print("Learned bias:", b_learned_rescaled)
print("True weights:", true_w.numpy())
print("True bias:", true_b)
The following figure shows the actual output after running the code.
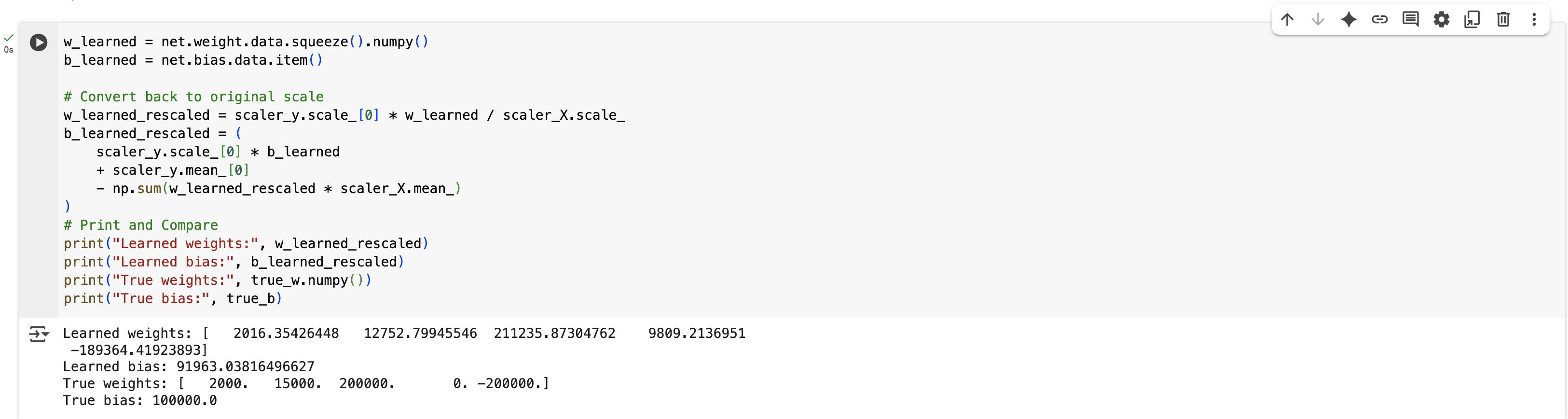
Even though this is a simple linear model, the results show that linear regression can effectively capture patterns in structured data.
For more accurate predictions — especially in real-world tasks — we would need to go further:
- Tune hyperparameters
- Optimize training
- Consider more advanced models (like adding regularization or nonlinear features)
It is a great first step in understanding and applying linear regression!
Part 8: Predicting a New Housing Sample
Finally, we test the trained model on a new house sample (area=200m², 3 bedrooms, detached type) to demonstrate real prediction.
# area=200m², 3 beds, detached
x_new = torch.tensor([[200.0, 3.0, 1.0, 0.0, 0.0]])
pred_price = net(x_new).item()
print("Predicted Price ≈ $", round(pred_price, 2))
Here are the result:

FAQ
Q: What features are used for this housing price prediction model?
A: We use multiple features: area (m²), number of bedrooms, and house type (detached, townhouse, condo).
Q: Why do we need to standardize the data?
A: Standardization helps each feature contribute equally and prevents large-valued features (like area) from dominating the regression.
Q: Can I extend this model with more features?
A: Yes. You can add more features such as location, year built, or amenities, and PyTorch will scale to handle them.